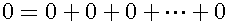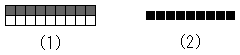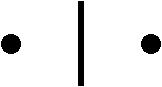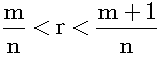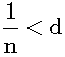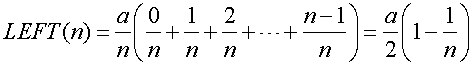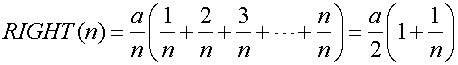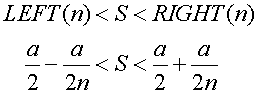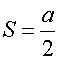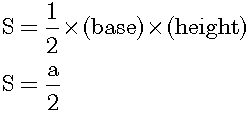Why did Euclid use two kinds of lines together? Let us consider this question.
The primary visual cortex plays the main role on this problem. The important purpose of the visual perception is
the extraction of the edge of the object.
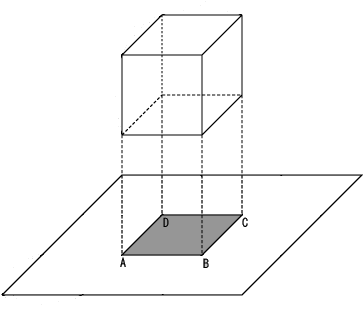 Figure6
Figure6
Figure 5 shows a cube and its shadow. The shadow is square ABCD. Each side corresponds to the edge of the shadow. It corresponds to the edge of the object. Each line is the borderline of the dark area and the light area. It is the
Euclidean line.
Simple cells in the primary visual cortex respond to it.
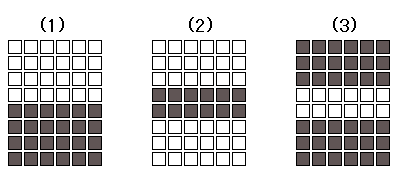 Figure7
Figure7
Figure 7 shows receptive fields of simple cells
[1] [2]. Figure 7-1 is the borderline between the dark area and the light area. Figure 7-2 is the dark bar. Figure 7-3 is the light bar. In this stage of visual perception, the line is the most important element. In contrast, the area is the most important element in the retina. The inversion of the figure and the ground occur in the primary visual cortex. The line becomes the figure from the ground.
As a result, human beings can easily recognize line drawings. Primitive men drew line drawings in
prehistoric cave paintings. The cartoon is also very popular in today. So Euclid might regard the line as important. The paper and pencil geometry has inherited this tradition. Thus, Euclid could not eliminate the pixelated line, because it is necessary to draw a line with a pencil.
The Line and the Area
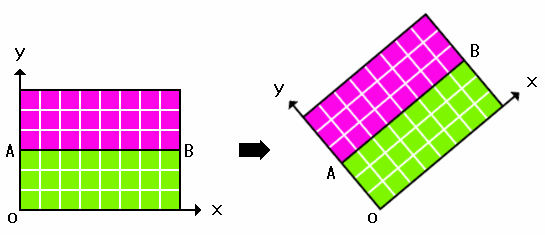
Finally, we shall consider definition 5. Euclid might have wanted to define area by length and width. However, the question what are length and width is still unsolved. For solving this question, we have to start with the unit square. If we accept the unit square, we can naturally derive length and breadth from the number of unit squares. Figure 6 shows the 5X4 rectangle as an example.
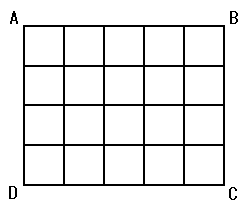 Figure8
Figure8
The rectangle contains 5X4 unit squares. The length of one side of the unit square is 1 and the area of the unit square is 1. So, we can easily derive the length and the area from the number of unit square. The length of the line AB is 5 and BC is 4. The area of the rectangle ABCD is 20.
We can easily define the area with the unit square. However, it is almost impossible to define the area without the unit square. Firstly, the area cannot be constructed, no matter how many points are collected.
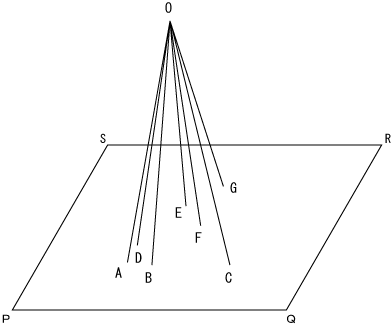 Figure9
Figure9
Figure 7 shows the point O and the plane PQRS. Points A to G are points on the plane PQRS. Consider the line AO. There is one-to-one correspondence between the point A and the point O. Equally, the point O corresponds to all points of the point A to the points G. Even if points on the plane increase, the point O corresponds to an arbitrary number of points. So the point O can be divided without limit. Thus, the plane does not consist of points.
Secondly, the area cannot be constructed, no matter how many lines are collected.
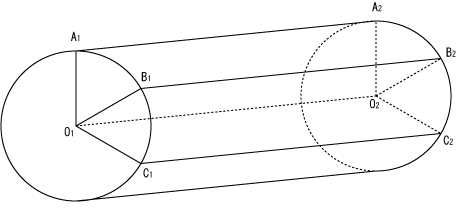 Figure10
Figure10
Figurer 8 shows the cylinder. Centers of two bases are the point O
1 and the point O
2. The line O
1O
2 parallels to the line A
1A
2, the line B
1B
2 and the line C
1C
2. Consider the rectangle O
1A
1A
2O
2. The line O
1O
2 corresponds to the line A
1A
2. Even if lines on the side face increase, the line O
1O
2 corresponds to an arbitrary number of lines on the side face. Of course, the line O
1O
2 has no area. No matter how many lines on the side face are collected, the total area of lines is zero. Thus, the side face does not consist of lines.
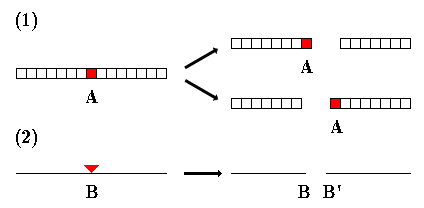
The most serious problem of Euclidean geometry is clarified. The whole doesn't consist of elements in Euclid's Elements. That is, the area doesn't consist of lines, and the line doesn't consist of points. Let us consider the relationship between the line and the point. Two points are arisen from the cut of the line. However, they have no length. Furthermore, the total length of the two lines is equal to the length of the original line. That is, the total length of resultant lines is constant, no matter how many times the line is cut. Even if we collect many points, any length cannot be generated. Hence, the line cannot be composed of points. Similarly, the area cannot consist of lines. Therefore, Euclidean figures cannot be constructed from elements. Why it cannot be constructive?
The configuration of Euclidean geometry is due to our visual brain. Especially, the primary visual cortex is the most important. The simple cell in it recognize the Euclidean line, which has no width. Against expectations, it is the blank of pixels. Figure-ground reversal occurs in this stage of our visual cognition. Then, pixels are concealed. Because we cannot see pixels, Euclidean geometry was built without them. Still, they exist implicitly. So, we can recognize the length and the area based on the number of them. As a consequence of the above discussion, if we want to make the constructive geometry, we need some kind of the pixel.
Firstly, we choose the unit square as the pixel, because it is compatible with Cartesian coordinate system. Then, the area is defined as the number of unit squares. Subsequently, length and width can be defined naturally. We can construct geometry based on the unit square. Such geometry is enough to apply to reality with a computer. I name it the pixelated geometry in
The Biological Foundation of Geometry. Then, we can estimate the Euclidean figure by pixels as precise as we want. Figure 11 shows the approximation of the right isosceles triangle. We can make the approximation of it by decreasing the size of the pixel as correct as we want. The pixelated geometry is enough practical.
 Figure11
Figure11
If we want to apply geometry to the real world, we must use the pixelated geometry. In fact, measurement error must exist. There is a limit of the precision of the measurement. So, no measurement is completely precise. Thus, we use significant figures in practical sciences. This solution is practically identical to use the pixelated geometry. Hence, the pixelated geometry is the interface between the Euclidean geometry and the real world.
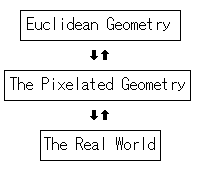 Figure12
Figure12
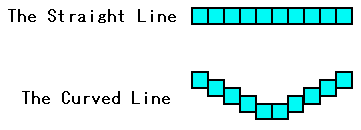
Figure 12 shows the scheme of the relationship among Euclidean geometry and the pixelated geometry and the real world. Now, we can realize why Euclid allowed the double meaning of the line. Because the Euclidean line has no width, we cannot draw it. Instead, we can draw the pixelated line. So the black line consists of black dots of the graphite in the traditional paper and pencil geometry. Figure 13 shows the relationship between the Euclidean line and the pixelated line.
 Figure13
Figure13
Figure 13-1 shows the gray area of the triangle, and Figure 13-2 shows the black line drawing of the triangle. At a glance, the edge of the gray triangle seems Euclidean line. However, it isn't the true Euclidean line. Rather, it is the pseudo-Euclidean line. The reason is as follows. As shown in
figure 7, there are three types of simple cells in the primary visual cortex. One type of them recognizes the edge, and another type of them recognizes the pixelated line. Both types of them correspond to many photoreceptor cells. Hence, they are constructed from many pixels. Next, the edge and the line are idealized and magnified in figure 14.
 Figure14
Figure14
Figure 14-1 shows pixels, which are the minimum requirements for the edge. It is the borderline between the gray area and the white area. Itself has no width. However, it needs at least two pixels in order to exist. Figure 14-2 shows the black pixelated line, which has the minimum width. Consequently, even if considering the ultimately idealized case, the edge and the line are constructed from pixels.
Now, we cannot know to what extent Euclid understood the problem. He knew at least the necessity of the pixelated geometry for applying Euclidean geometry to the real world. When anyone wants to draw a figure for the traditional paper and pencil geometry, he will notice the requirement of it.
The next step is the Euclidean geometry without curves. It is the necessary result of definitions of Euclid's Elements. Firstly, following two definitions define a point. According to the definition 3, the ends of a line are points. According to the definition 2, a line is breadthless length. Hence, a point has no length and no width. That is, it has no extent. Secondly, let us consider two points. If there is a distance between them, we can draw a straight line between them. However, if there is no distance between them, they must be the same point. Hence, the length is the length of the straight line. Thirdly, let us consider a length of a curved line. If two points on it are discrete, the distance of them is the length of the straight line between them. If two points are attached, they are the same point. Hence, the true length of the curved line cannot exist. Moreover, because a line cannot be composed of points, we have no means to compose a curved line. Rather, it is preexistent in the idea world. At least, we cannot determine the true length of it. Thus, if we want to construct the true quantitative geometry, we must exclude curved lines.
Euclidean geometry without curves is compatible with the pixelated geometry. Firstly, the physiological necessity is as follows. Because simple cells of the primary visual cortex recognize the straight line, it is the basic element of the human visual image. Secondly, the borderline between two pixels must be it in general. Figure 12 shows that the straight borderline between two adjacent pixels. Two black circles are centers of them. Because distances of a point on a borderline from each center are equal, the borderline must be straight.
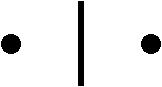 Figure15
Figure15
Next, let us try to quantify Euclidean geometry without curves. If it is connected with the pixelated geometry, it will become the quantitative geometry. Figure 16 shows the division of the rectilinear figure into the elementary figures.
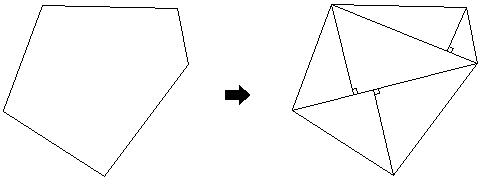 Figure16
Figure16
Any polygon can be divided into triangles. Likewise, any triangle can be divided into two rectangular triangles. It is the elementary figure of the geometry, which consists of only rectilinear figures. Next basic figure is the rectangle, which consists of two congruent rectangular triangles. It is the elementary figure of the quantitative geometry. So, its area can be found by multiplying the base times the height. Then, we shall use the changeable sized pixels in order to make the approximation of it. If the value of the ratio of its height to its base is the irrational magnitude r, then it cannot be divided into unit squares. Instead, we can make the approximation of it by them. If we choose a unit square, whose sides equal 1/n. Then, we can estimate it by unit squares as figure 17.
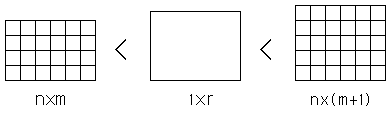 Figure17
Figure17
There is a natural number m such that:
Then, we can make the approximation of r by decreasing the size of the pixel as precise as we want. That is, we can approximate any irrational magnitude to the arbitrary precision of d. If we want to decrease the error to less than d, we can increase n such that:
So, we can always achieve the necessary accuracy of the approximation. Therefore, Euclidean geometry without curves is compatible with the pixelated geometry.
Euclidean Geometry with Curves
The next step is the Euclidean geometry with curves. The curve itself is the paradoxical figure. As mentioned in
Euclidean geometry without curves, the length of the curve cannot be defined. However, Euclid circumvented this problem, and he defined the circle as follows.
Definition 15: A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another.
Euclid assumed the preexisting circle, and then he describes the position of a point on it. It seems that the sequence of the definition is reversed. So, his definition is acrobatic. However, it is biologically reasonable solution. Our brain constructs the curve from very many pixels. For example, figure 18 shows the construction of the circle.
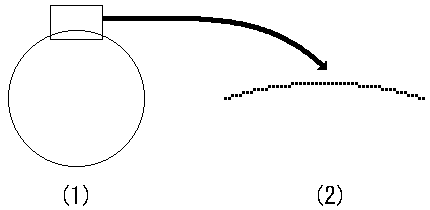 Figure18
Figure18
Figure 18-1 shows the circle. A part of it is expanded in figure 18-2. This figure represents that the circle is constructed from a lot of pixels in the wide area. Indeed, figures, which contain curved lines, is recognized in higher visual areas of the brain
[3] [4]. Firstly, the human brain makes the circle from the vast number of pixels. Secondary, it conceals them, and then it shows us the circle. Therefore, even though Euclid didn't know the neuroscience, he created the sophisticated definition of the circle. However, the length of the curve cannot be determined. It can be only approximated by using straight lines. Figure 19 shows an example. It represents Archimedes’approximation of pi.
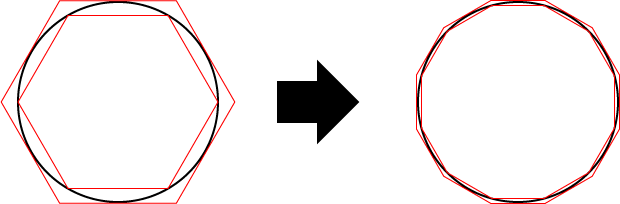 Figure19
Figure19
It shows that the circle is interposed between the inscribed polygon and circumscribed polygon. The left side of it is hexagon, and the right side of it is dodecagon. The circumference of the circle is greater than the perimeter of the inscribed polygon and less than the perimeter of the circumscribed polygon. Archimedes got a doubling of sides of hexagon, and then he got dodecagon. He repeated doubling. Finally, he approximated the circumference of the circle by using 96-sided polygon.
Additionally, The important fact must be reconfirmed. The length of the circumference of the circle cannot be directly defined. It is only approximated by using the total length of straitht lines. That is, it isn't the fixed value. Of course, pi isn't an algebraic number. Moreover, unless a limit is used, it cannot be represented by any formula. In contrast, the square root of two is the fixed value. It is the length of the straight line in Euclidean geometry.
Next, let us make the approximation of the area enclosed by the curves by rectangles, which are the basic figure of the quantitative geometry. When we use Cartesian coordinates, the problem is converted into the approximation of the area under the curve. Figure 19 shows an example.
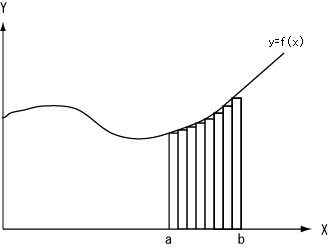 Figure20
Figure20
We shall estimate the area between the x-axis and the graph of y=f(x) in [a,b]. It is divided into n rectangles, whose width is (b-a)/n. If we increase n, the error will be decreased. This is the idea of the definite integral. Figure 13 shows the simplest example of it.
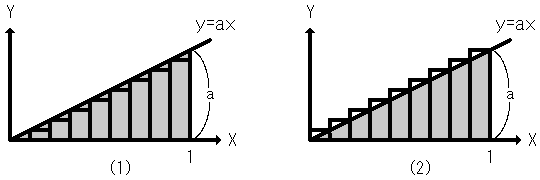 Figure21
Figure21
Let us calculate the area under the graph of y=ax in [0,1] using the definite integral. The target area represents the gray triangle. Firstly, the interval zero to one is divided equally into n subintervals. Next, we estimate the gray area by n rectangles. Then, the width of each rectangle is 1/n. Next, we choose the height of each rectangle as the value of the function at the left end point of each subinterval. Next, we number rectangles consequently from left to right. The height of the m-th rectangle is a(m-1)/n. Then, the total area of all rectangles is called left sum:
Next, we choose the height of each rectangle as the value of the function at the right end point of each subinterval. The height of the m-th rectangle is am/n. Then, the total area of all rectangles is called right sum:
We assume that the are of gray triangle is S. Then, because y=ax is the monotonically increasing function, the next inequality is formed:
Next, let us consider the pixelated geometry. Because it is the interface of the real world, the calculation result of any kind of geometry must be converted into that of it. If we need the precision of d. A magnitude, which is sufficiently smaller than d, can be ignored in the pixelated geometry. In this case, we can decrease a/2n as small as we want. So, we can make it sufficiently smaller than any d. Consequently, when we ignore a/2n, S is estimated at a/2:
We can estimate the are of the gray triangle using the integral in the pixelated geometry. Meanwhile, in Euclidean geometry, it is easily calculated by the next formula:
Therefore, the result of the definite integral is consistent with the result of the calculation in Euclidean geometry.
Conclusion
Now, we have constructed the bridge between the number theory and the geometry. The most prominent feature of it is that it doesn't contain the infinity or the infinitesimal. The mystique of the mathematics is largely due to them. So, we have demystified the geometry by excluding them. This is the first step of the revolution of mathematics. It must be reconstructed based on the neuroscience. The reason is as follows.
Our brain isn't intelligently designed. There is no logical blue print. Professor Linden says in "The Accidental Mind: How Brain Evolution Given Us Love, Memory, Dreams and God."
What I hope to show here is that as every level of brain organization, from regions and circuits to cells and molecules, the brain is inelegant and inefficient agglomeration of stuff, which nonetheless work surprisingly well. The brain is not the ultimate general-purposed computer. It was not designed at once, by a genius, on a blank piece of a paper. Rather, it is a very peculiar edifice that reflects millions of years of evolutionary history. In many cases, the brain has adopted solutions to particular problems in the distant past that have persisted over time and have been recycled for other uses or have severely constrained the possibilities for further change. In the word of the pioneering molecular biologist Francois Jacob, "Evolution is a tinkerer, not an engineer."
He says that our brain is the result of the serendipitous evolution. That is, our geometry is built on the visual brain, which is the great piles of ad-hoc solutions. As a logical consequence, our constructive geometry is the patchwork of three geometries: pixelated geometry, Euclidean geometry without curves and Euclidean geometry with curves. Moreover, the connection of them is incomplete.
Since Euclidean geometry is made based on the information processing of the visual brain, it contains internal contradictions. Nevertheless, it is enough if it can be used well. When we apply it to the reality, it must be converted into pixelated geometry. Because
the natural number one is the foundation of the cognition of a life, the number theory is the base of all mathematics. Furthermore, digital information consists of natural numbers. The original form of it is DNA, which determines the survival rate of a life. So, we have constructed the conjunction of Euclidean geometry to the number theory. However, it depends on the approximation. That is, it is incomplete. Even so, we must not pursuit the completeness of it, because our brain wasn't constructed based on the logical blue print. Rather, if we acquired the logical completeness of it by force, our logic itself would be broken. So, our solution uses the approximation, which is the realistic compromise. As a result, Euclidean geometry is loosely connected with the number theory.
Moreover, all fields of mathematics must be connected to the number theory. Ancient Greeks wanted to do this task. However, they failed, because they aspired for the tight connection. Instead, we must set forth a goal of the loose connection, because our brain is the kludge, and it is not logically designed. Naturally, other mathematical fields need to be reexamined. Just now, this is the beginning of the revolution of the mathematics. Shall we participate in it?
References
1. D. H. Hubel, T. N. Wiesel,
Receptive Fields of Single Neurons in the Cat's Striate Cortex. J. Physiol. 148, 574-579 (1959)
2. D. H. Hubel, T. N. Wiesel,
Receptive Fields and Functional Architecture of Monkey Striate Cortex. J. Physiol. 195, 215-243 (1968)
3. P. Girard, S. G. Lomber, J. Bullier,
Shape Discrimination Deficits During Reversible Deactivation of Area V4 in the Macaque Monkey. Cerebral Cortex 12, 1146-1156 (2002)
4. H. O. Karnath, J. Rüter, A. Mandler, M. Himmelbach,
The Anatomy of Object Recognition—Visual Form Agnosia Caused by Medial Occipitotemporal Stroke. J. Neuroscience 29, 5854-5862 (2009)
Table of Contents